1.冒泡排序
- 步骤1: 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 步骤2: 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- 步骤3: 针对所有的元素重复以上的步骤,除了最后一个;
- 步骤4: 重复步骤1~3,直到排序完成。
func BubbleSort(array *[]int) {
if array == nil {
return
}
length := len(*array)
for i := 0; i < length -1; i++ {
flag := false
for j := 0; j < length -1; j++ {
if (*array)[j+1] < (*array)[j] {
(*array)[j], (*array)[j+1] = (*array)[j+1], (*array)[j]
flag = true
}
}
if !flag {
break
}
}
}2.选择排序
n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下:
- 步骤1:初始状态:无序区为R[1…n],有序区为空;
- 步骤2:第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1…i-1]和R(i…n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1…i]和R[i+1…n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
- 步骤3:n-1趟结束,数组有序化了。
func SelectSort(array *[]int) {
if array == nil {
return
}
length := len(*array)
for i := 0; i < length-1; i++ {
for j := i + 1; j < length; j++ {
if (*array)[j] <= (*array)[i] {
(*array)[i], (*array)[j] = (*array)[j], (*array)[i]
}
}
}
}3.插入排序
一般来说,插入排序都采用in-place在数组上实现。具体算法描述如下:
- 步骤1: 从第一个元素开始,该元素可以认为已经被排序;
- 步骤2: 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 步骤3: 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 步骤4: 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 步骤5: 将新元素插入到该位置后;
- 步骤6: 重复步骤2~5。
func InserSort(array *[]int) {
if array == nil {
return
}
length := len(*array)
for i := 0; i < length; i++ {
for j := i; j > 0; j-- {
if (*array)[j] < (*array)[j -1] {
(*array)[j], (*array)[j -1] = (*array)[j-1], (*array)[j]
}
}
}
}4.希尔排序
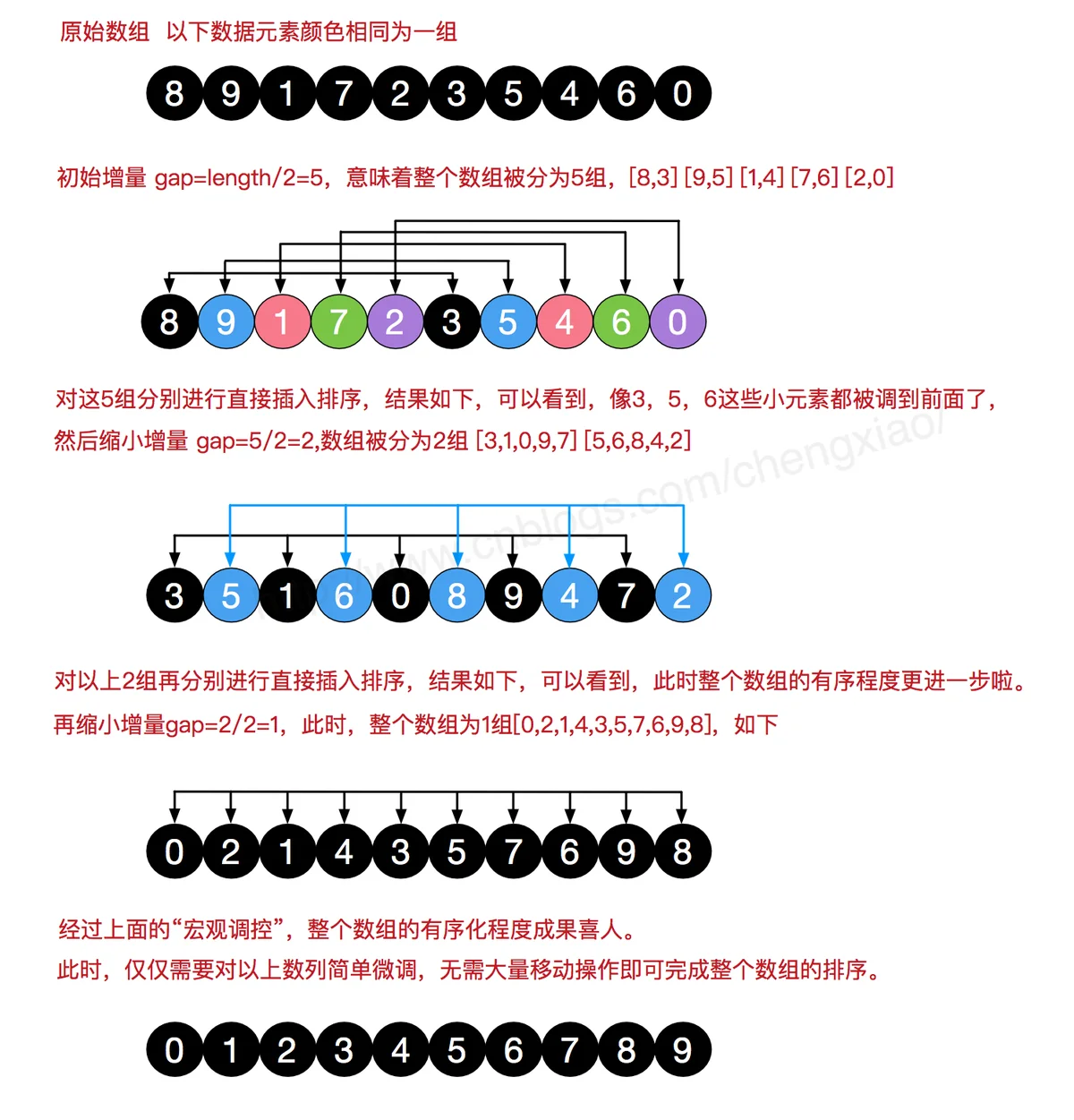
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,具体算法描述:
- 步骤1:选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
- 步骤2:按增量序列个数k,对序列进行k 趟排序;
- 步骤3:每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
5.归并排序
- 步骤1:把长度为n的输入序列分成两个长度为n/2的子序列;
- 步骤2:对这两个子序列分别采用归并排序;
- 步骤3:将两个排序好的子序列合并成一个最终的排序序列。
//归并
func merge(array *[]int, left, right int) {
begin1 := left
end1 := (left + right) / 2
begin2 := end1 +1
end2 := right
pTemp := make([]int, right - left +1)
count := 0
//合并有序数组
for begin1 < end1 && begin2 < end2 {
if (*array)[begin1] < (*array)[begin2] {
pTemp[count] = (*array)[begin1]
begin1++
} else {
pTemp[count] = (*array)[begin2]
begin2++
}
count++
}
for begin1 <= end1 {
pTemp[count] = (*array)[begin1]
begin1++
count++
}
for begin2 <= end2 {
pTemp[count] = (*array)[begin2]
begin2++
count++
}
count = 0
for i := left ; i < right - left + 1; i++ {
(*array)[i] = pTemp[count]
count++
}
}
func MergeSort(array *[]int, left, right int ) {
if array == nil {
return
}
mid := (left + right) / 2
if left < right {
//拆分
MergeSort(array, left, mid)
MergeSort(array, mid + 1 , right)
//合并
merge(array, left, right)
}
}6.快排
快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。具体算法描述如下:
- 步骤1:从数列中挑出一个元素,称为 “基准”(pivot );
- 步骤2:重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 步骤3:递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
func quickSortPartition(array *[]int, left int, right int) int {
temp := (*array)[left]
i := left +1
j := right
for i < j {
for (*array)[j] > temp{
j--
}
for (*array)[i] < temp {
i++
}
if i < j {
(*array)[i], (*array)[j] = (*array)[j], (*array)[i]
continue
}
i++
}
(*array)[j], (*array)[left] = (*array)[left], (*array)[j]
return j
}
func QuickSort(array *[]int, left int, right int) {
length := len(*array)
if length <= 0 || left < 0 || right > length - 1 || left > right{
return
}
partition := quickSortPartition(array, left, right)
QuickSort(array, left, partition -1)
QuickSort(array, partition + 1, right)
}7.堆排
- 步骤1:将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
- 步骤2:将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
- 步骤3:由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。

// 小根堆
//length--需要调整的长度,index--第一个非叶子节点坐标
func adjust(array *[]int, length int, index int) {
indexLeft := 2 *index +1
indexRight := 2 *index +2
maxIndex := index
if indexLeft < length && (*array)[indexLeft] > (*array)[maxIndex] {
maxIndex = indexLeft
}
if indexRight < length && (*array)[indexRight] > (*array)[maxIndex] {
maxIndex = indexRight
}
if maxIndex != index {
(*array)[maxIndex], (*array)[index] = (*array)[index], (*array)[maxIndex]
adjust(array, length, maxIndex)
}
}
func HeapSort(array *[]int) {
if array == nil {
return
}
length := len(*array)
//构建大顶堆
for i := length/2 -1; i >= 0; i-- {
adjust(array, length, i)
}
//调整大顶堆,交换堆尾和堆首
for i := length -1; i > 0; i-- {
(*array)[0], (*array)[i] = (*array)[i], (*array)[0]
//重建大顶堆,将前面无序堆调整成大顶堆
adjust(array, i, 0)
}
}
