冒泡排序算法的原理如下:
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
代码实现:
func maopao(arr []int)[]int{
var tmp int
for i:=0;i<len(arr)-1;i++{
for j:=0;j<len(arr)-i-1;j++{
if arr[j]>arr[j+1]{
tmp=arr[j]
arr[j]=arr[j+1]
arr[j+1]=tmp
}
}
}
return arr
}
优化方式
1、优化外层循环,引入一个标签flag,在排序过程中若发生了交换则将flag置为1,各趟排序结束时检查flag,若未曾发生过交换说明已经有序,则终止算法,不再进行下一趟排序。代码如下:
func maopao(arr []int)[]int{
var tmp int
for i:=0;i<len(arr)-1;i++{
falg:=0//每次遍历标志位都要先置为0,才能判断后面的元素是否发生了交换
for j:=0;j<len(arr)-i-1;j++{
if arr[j]>arr[j+1]{
tmp=arr[j]
arr[j]=arr[j+1]
arr[j+1]=tmp
falg=1
}
}
if falg==0{
break
}
}
return arr
}
2、优化内层循环,在每趟扫描中,记住最后一次交换发生的位置lastExchange,(该位置之后的相邻记录均已有序),可以减少排序的趟数。
func maopao(arr []int)[]int{
var tmp int
k:=len(arr)-1
var pos int
for i:=0;i<len(arr)-1;i++{
falg:=0//每次遍历标志位都要先置为0,才能判断后面的元素是否发生了交换
for j:=0;j<k;j++{
if arr[j]>arr[j+1]{
tmp=arr[j]
arr[j]=arr[j+1]
arr[j+1]=tmp
falg=1
pos = j //循环里最后一次交换的位置 j赋给pos
}
}
if falg==0{
break
}
k=pos //将pos赋给k
}
return arr
}
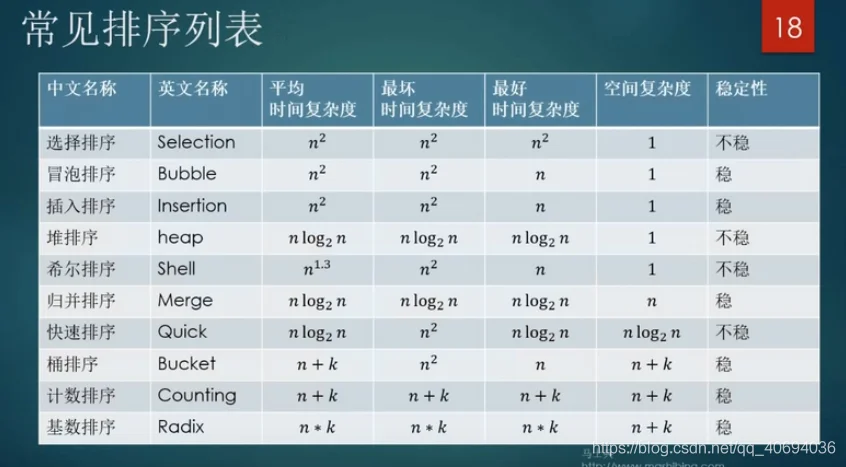
快速排序使用分治的思想,通过一趟排序将待排序列分割成两部分,其中一部分记录的关键字均比另一部分记录的关键字小。之后分别对这两部分记录继续进行排序,以达到整个序列有序的目的。
挖坑填补法
首先,我们仍然是从end开始向前找一个小于28的数,找到后直接放在begin的位置,注意这里不是交换,如下图

箭头所指向的是我们选取的基准值,这时可以理解为它不在这个数列当中,而end对应的位置就出现了一个坑,这时,begin开始向后寻找,找到第一个大于基准值的数后放到end的位置,如下图

此时,begin的位置又会出现一个坑,这时再次让end向前移动继续找第一个小于基准值的数,放到begin的位置,再使begin向后移动找第一个大于基准值的数,重复此操作直到begin和end相遇,这时,把基准值放到该位置。这样,一趟快速排序结束,如下图
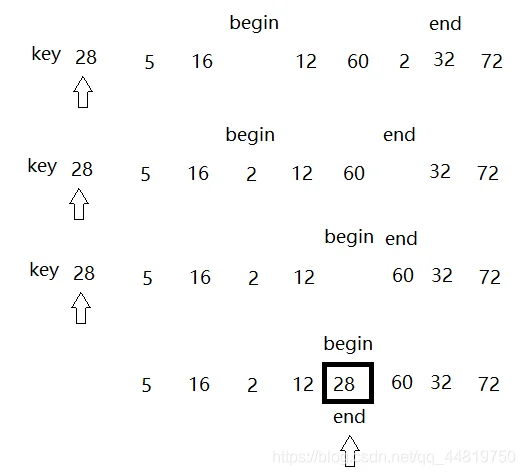
此时,28的前面都是小于它的数,其后面都是大于它的数,则28的位置确定,只需要递归进行快排后,就会变成一个有序数列
代码如下:
func main(){
arr:=[]int{4,8,2,1,6,9,3,5,7,8,1,4}
arr=quick(arr,0,len(arr)-1)
fmt.Println(arr)
}
选第一个数为基准数
func quick(arr []int,low,high int)[]int{
if low>high{
return arr
}
i:=low
j:=high
t:=arr[i]
for i<j{
for i<j&&arr[j]>=t{
j--
}
arr[i]=arr[j]
for i<j&&arr[i]<=t{
i++
}
arr[j]=arr[i]
}
arr[i]=t
quick(arr,low,i-1)
quick(arr,i+1,high)
return arr
}
选择最后一个数为基准数
func quick(arr []int,start int,end int)[]int{
if end<start{
return arr
}
i,j:=start,end
t:=arr[j] //这里将最后一个元素设为基准数
for j>i{
for j>i&&arr[i]<=t{ //要先找前面的,再找后面的
i++
}
arr[j]=arr[i]
for j>i&&arr[j]>=t{
j--
}
arr[i]=arr[j]
}
arr[j]=t
quick(arr,start,i-1)
quick(arr,i+1,end)
return arr
}
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。
插入排序基本思想是将一个记录插入到已经排好序的有序表中,从而得到一个新的、记录数增1的有序表。
func main(){
arr:=[]int{4,8,2,1,6,9,3,5,7,8,1,4}
arr=charu(arr)
fmt.Println(arr)
}
func charu(arr []int)[]int{
if len(arr)<2{
return arr
}
for i:=1;i<len(arr);i++{
for index:=i;(index>0)&&(arr[index]<arr[index-1]);index--{
//这里index>0 必须在前面,
//如果写成(arr[index]<arr[index-1])&&index>0会报错
arr[index],arr[index-1]=arr[index-1],arr[index]
}
}
return arr
}
func main(){
arr:=[]int{9,5,7,4,8,6,3,2,1}
n:=len(arr)-1
mergesort(arr,0,n)
fmt.Println(arr)
}
func mergesort(arr []int,start,end int){ //分割,直到分成每堆只有2个元素
if end <= start{
return
}
mid:=(start+end)/2
mergesort(arr,start,mid)
mergesort(arr,mid+1,end)
paixu(arr,start,mid,end)
}
func paixu(arr []int,start,mid,end int){ //把两个有序数组合并成一个
temp:=[]int{}
left := start
right := mid+1
for left<=mid && right<=end{
if arr[left]<=arr[right]{
temp=append(temp,arr[left])
left++
}else{
temp=append(temp,arr[right])
right++
}
}
for left<=mid{
temp=append(temp,arr[left])
left++
}
for right<=end{
temp=append(temp,arr[right])
right++
}
for k,v:=range temp{
arr[start+k]=v
}
}
堆排序的基本思想是:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了
package main
import "fmt"
func main(){
arr:=[]int{4,8,2,1,6,9,3,5,7,8,1,4}
dui(arr)
fmt.Println(arr)
}
func swap(arr []int,a,b int){
arr[a],arr[b]=arr[b],arr[a]
}
func heapadjust(arr []int,i,m int){
son:=i*2+1
for son<m{
if son+1<m&&arr[son]<arr[son+1]{//首先判断选出左节点大还是右节点大
son++
}
if arr[i]>arr[son]{
break
}else{
swap(arr,i,son)
i=son
son=i*2+1
}
}
}
func dui(arr []int){
for i:=len(arr)/2-1;i>=0;i--{ //这里是先变成大顶堆
heapadjust(arr,i,len(arr))
}
for i:=len(arr)-1;i > 0;i--{
//将最大值与最后一个交换,然后对前i-1重新排序
swap(arr,0,i)
heapadjust(arr,0,i-1)
}
}
都是分治法的应用,将原问题分解成一系列子问题。
快速排序是自顶向下,分解然后排序,因为就地排序不用合并。
归并排序是自底向上,先分解成不能再分然后排序将两个已排序的合并。
归并排序更稳定,因为相同的元素的位置不会被改变。快速排序不稳定是因为元素交换是跨元素的,相邻相同元素可能发生位置交换
快排稳定版稳定 指:数组中具有相同元素,排序过后这些元素相对次序保持不变,则稳定
思路:
新创建一个辅助数组,原数组只保存不需要交换的元素,将要交换的元素放到辅助数组中,最后再合并起来避免交换。
