1. 快速排序
思路和算法
快速排序的主要思想是通过划分将待排序的序列分成前后两部分,其中前一部分的数据都比后一部分的数据要小,然后再递归调用函数对两部分的序列分别进行快速排序,以此使整个序列达到有序。
快排模板1:

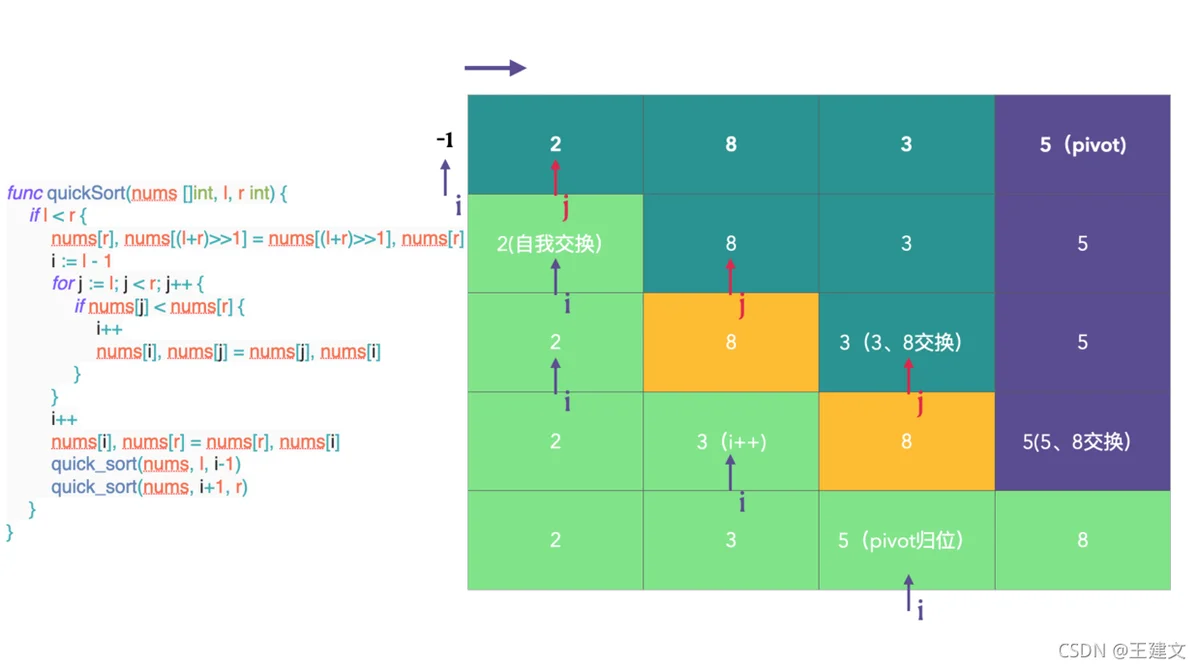
func quick_sort(nums []int, l, r int) {
if l >= r {
return
}
rand.Seed(time.Now().Unix())
p := rand.Intn(r-l+1) + l
nums[r], nums[p] = nums[p], nums[r]
i := l - 1
for j := l; j < r; j++ {
if nums[j] < nums[r] {
j++
nums[i], nums[j] = nums[j], nums[i]
}
}
nums[i+1], nums[r] = nums[r], nums[i+1]
quick_sort(nums, l, i-1)
quick_sort(nums, i+1, r)
}
复杂度分析
-
时间复杂度:基于随机选取主元的快速排序时间复杂度为期望 O(nlogn),其中 n 为数组的长度。
-
空间复杂度:O(h),其中 h 为快速排序递归调用的层数。我们需要额外的O(h) 的递归调用的栈空间,由于划分的结果不同导致了快速排序递归调用的层数也会不同,最坏情况下需 O(n) 的空间,最优情况下每次都平衡,此时整个递归树高度为nlogn,空间复杂度为 O(logn)。
不稳定
快排模板2:
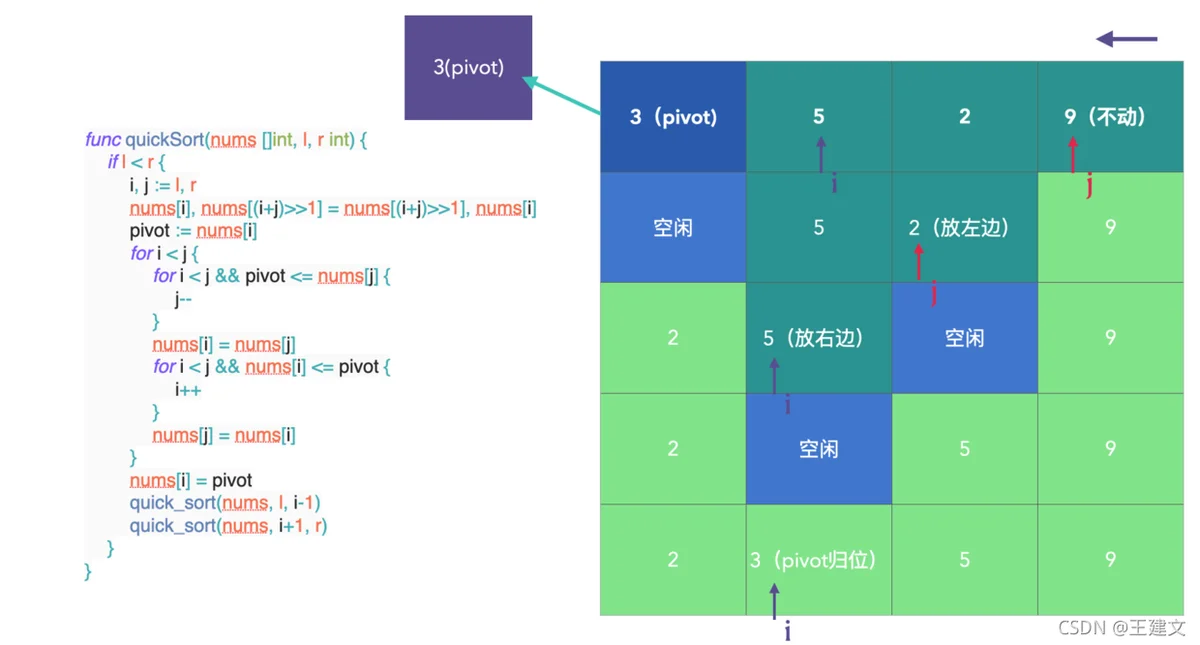
func quick_sort(nums []int, l, r int) {
if l >= r {
return
}
i, j := l, r
nums[i], nums[(i+j)>>1] = nums[(i+j)>>1], nums[i]
pivot := nums[i]
for i < j {
for i < j && pivot <= nums[j] {
j--
}
nums[i] = nums[j]
for i < j && nums[i] <= pivot {
i++
}
nums[j] = nums[i]
}
nums[i] = pivot
quick_sort(nums, l, i-1)
quick_sort(nums, i+1, r)
}
快排模板3:
确定pivot,小于pivot放左边,大于pivot放右边,pivot已归位
递归求pivot左边、右边

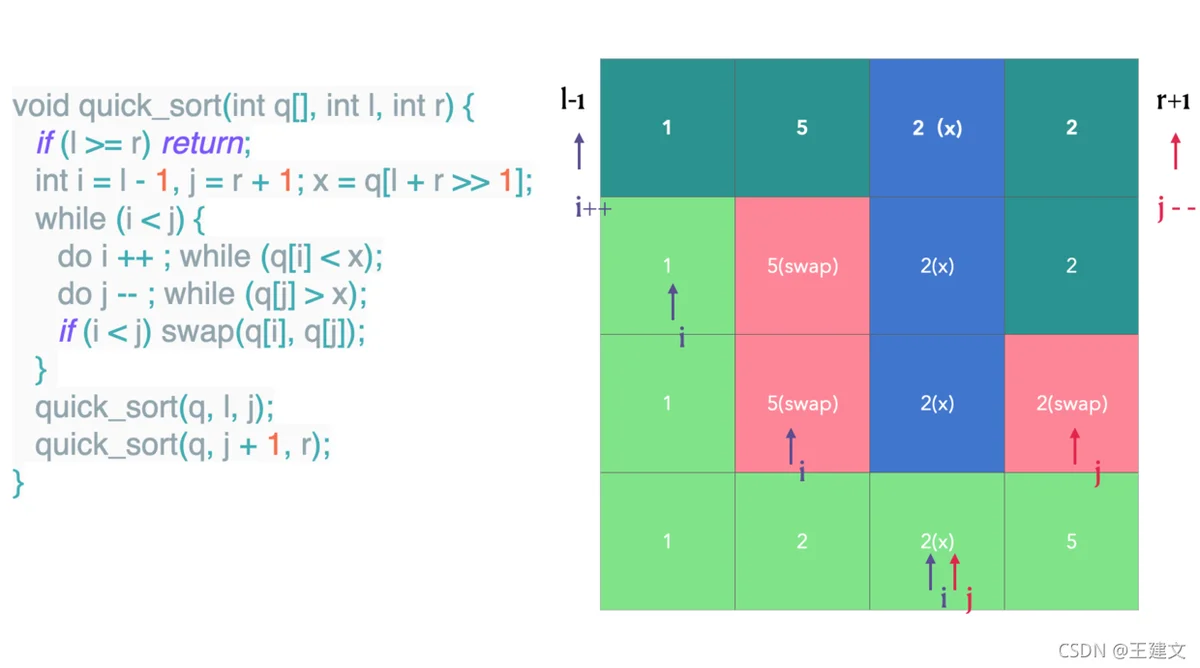
func quickSort(q []int, l, r int) {
if l >= r { // 终止条件
return
}
x := q[(l+r)>>1] // 确定分界点
i, j := l-1, r+1 // 两个指针,因为do while要先自增/自减
for i < j { // 每次迭代
for { // do while 语法
i++ // 交换后指针要移动,避免没必要的交换
if q[i] >= x {
break
}
}
for {
j--
if q[j] <= x {
break
}
}
if i < j { // swap 两个元素
q[i], q[j] = q[j], q[i]
}
}
quickSort(q, l, j) // 递归处理左右两段
quickSort(q, j+1, r)
}
2.归并排序
思路
归并排序利用了分治的思想来对序列进行排序。对一个长为 n 的待排序的序列,我们将其分解成两个长度为 n/2的子序列。每次先递归调用函数使两个子序列有序,然后我们再线性合并两个有序的子序列使整个序列有序。
求mid,递归排左边、右边,合并
func merge_sort(nums []int, l, r int) {
if l < r {
mid := (l + r) >> 1
merge_sort(nums, l, mid)
merge_sort(nums, mid+1, r)
i, j := l, mid+1
tmp := []int{}
for i <= mid || j <= r {
if i > mid || (j <= r && nums[j] < nums[i]) {
tmp = append(tmp, nums[j])
j++
} else {
tmp = append(tmp, nums[i])
i++
}
}
copy(nums[l:r+1], tmp)
}
}
func merge(nums []int, left, mid, right int) {
i, j := left, mid+1
tmp := []int{}
for i <= mid && j <= right {
if nums[i] < nums[j] {
tmp = append(tmp, nums[i])
i++
} else {
tmp = append(tmp, nums[j])
j++
}
}
if i <= mid {
tmp = append(tmp, nums[i:mid+1]...)
} else {
tmp = append(tmp, nums[j:right+1]...)
}
copy(nums[left:right+1], tmp)
// for k := 0; k < len(tmp); k++ {
// nums[left+k] = tmp[k]
// }
}
func mergeSort(nums []int, left, right int) {
if left < right {
mid := (left + right) / 2
mergeSort(nums, left, mid)
mergeSort(nums, mid+1, right)
merge(nums, left, mid, right)
}
}
func merge_sort(nums []int, left, right int) {
if left < right {
mid := (left + right) >> 1
merge_sort1(nums, left, mid)
merge_sort1(nums, mid+1, right)
tmp := []int{}
i, j := left, mid+1
for i <= mid && j <= right {
if nums[i] <= nums[j] {
tmp = append(tmp, nums[i])
i++
} else {
tmp = append(tmp, nums[j])
j++
}
}
if i <= mid {
tmp = append(tmp, nums[i:mid+1]...)
} else { //如果使用...运算符,可以将一个切片的所有元素追加到另一个切片里
tmp = append(tmp, nums[j:right+1]...)
}
copy(nums[left:right+1], tmp)
}
}
复杂度分析
-
时间复杂度:O(nlogn)。由于归并排序每次都将当前待排序的序列折半成两个子序列递归调用,然后再合并两个有序的子序列,而每次合并两个有序的子序列需要 O(n) 的时间复杂度,所以我们可以列出归并排序运行时间T(n) 的递归表达式:
T(n)=2T(n/2)+O(n)
根据主定理我们可以得出归并排序的时间复杂度为 O(nlogn)。 -
空间复杂度:O(n)。我们需要额外 O(n) 空间的 tmp 数组,且归并排序递归调用的层数最深为 log 2n,所以我们还需要额外的 O(logn) 的栈空间,所需的空间复杂度即为 O(n+logn)=O(n)。
稳定
3.堆排序
思路和算法
堆排序的思想就是先将待排序的序列建成大根堆,使得每个父节点的元素大于等于它的子节点。此时整个序列最大值即为堆顶元素,我们将其与末尾元素交换,使末尾元素为最大值,然后再调整堆顶元素使得剩下的 n−1 个元素仍为大根堆,再重复执行以上操作我们即能得到一个有序的序列。
func heap_sort(nums []int) []int {
lens := len(nums) - 1
for i := lens/2; i >= 0; i -- { // 建堆 O(n) lens/2后面都是叶子节点,不需要向下调整
down(nums, i, lens)
}
for j := lens; j >= 1; j -- {//堆排序(升序):堆顶(最大值)交换到末尾
nums[0], nums[j] = nums[j], nums[0]
lens --
down(nums, 0, lens)
}
return nums
}
func down(nums []int, i, lens int) {//O(logn)大根堆,如果堆顶节点小于叶子,向下调整
max := i
if i<<1+1 <= lens && nums[i<<1+1] > nums[max] {
max = i<<1+1
}
if i<<1+2 <= lens && nums[i<<1+2] > nums[max] {
max = i<<1 + 2
}
if max != i {
nums[max], nums[i] = nums[i], nums[max]
down(nums, max, lens)
}
}
复杂度分析
-
时间复杂度:O(nlogn)。初始化建堆的时间复杂度为 O(n),建完堆以后需要进行 n−1 次调整,一次调整(即 down) 的时间复杂度为 O(logn),那么 n−1 次调整即需要 O(nlogn) 的时间复杂度。因此,总时间复杂度为O(n+nlogn)=O(nlogn)。
-
空间复杂度:O(1)。只需要常数的空间存放若干变量。
不稳定
4.选择排序
从未排序序列中找到最小元素,存放到排序序列的起始位置
再从剩余元素中找到最小元素,存放到已排序序列末尾…
func select_sort(nums []int) {
for i := 0; i < len(nums)-1; i ++ {
minIdx := i
for j := i+1; j < len(nums); j ++ {
if nums[j] < nums[minIdx] { //找最小的数
minIdx = j //保存最小数索引
}
}
nums[i], nums[minIdx] = nums[minIdx],nums[i]
}
}
复杂度分析
- 时间复杂度:O(n ^2)
- 空间复杂度:O(1)
不稳定
5.插入排序
构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
选取数组第2个元素开始比较,如果左边第1个元素比它大,左边元素向右移动1位,索引减1,向前扫描…
直到左边元素比他小,插入这个元素右边
func insertSort(nums []int) []int {
n := len(nums)
for i := 1; i < n; i++ {
tmp := nums[i]
j := i - 1
for j >= 0 && nums[j] > tmp { //左边比右边大
nums[j+1] = nums[j] //右移1位
j-- //扫描前一个数
}
nums[j+1] = tmp //添加到小于它的数的右边
}
return nums
}
复杂度分析
- 时间复杂度:O(n ^2)
- 空间复杂度:O(1)
稳定
6.冒泡排序
冒泡排序是从左到右依次比较相邻的两个元素,如果前一个元素比较大,就把前一个元素和后一个交换位置,遍历数组之后保证最后一个元素相对于前面的永远是最大的。然后让最后一个保持不变,重新遍历前n-1个元素,保证第n-1个元素在前n-1个元素里面是最大的。依此规律直到第2个元素是前2个元素里面最大的,排序就结束了。
第1个元素比第2个元素大,交换…
func bubbleSort(nums []int) []int {
n := len(nums)
for i := 0; i < n - 1; i++ {
exchange := false
for j := 0; j < n-i-1; j++ {
if nums[j] > nums[j+1] { //两两比较,前面比后面大
nums[j], nums[j+1] = nums[j+1], nums[j] //交换
exchange = true
}
}
if !exchange {
return nums
}
}
return nums
}
复杂度分析
- 时间复杂度:O(n ^2)
- 空间复杂度:O(1)
稳定
7.希尔排序
第一个突破O(n^2)的排序算法,希尔排序就是为了加快速度简单地改进了插入排序,交换不相邻的元素以对数组的局部进行排序。
采⽤插入排序的⽅法,先让数组中任意间隔为 h 的元素有序,刚开始 h 的⼤大⼩小可以是 h = n / 2,接着让 h = n / 4,让 h ⼀一直缩⼩小,当 h = 1 时,也就是此时数组中任意间隔为1的元素有序, 此时数组就是有序的了。
func shell_sort(li []int) {
for gap := len(li) / 2; gap > 0; gap /= 2 {
for i := gap; i < len(li); i++ {
tmp := li[i]
j := i - gap
for j >= 0 && tmp < li[j] {
li[j+gap] = li[j]
j -= gap
}
li[j+gap] = tmp
}
}
}
复杂度分析
- 时间复杂度: O(nlogn)
- 空间复杂度: O(1)
不稳定
8.计数排序
把数组元素作为数组的下标,然后⽤一个临时数组统计该元素出现的次数,例如 cnt[i] = m, 表示元素 i 一共出现了 m 次。最后再把临时数组统计的数据从小到⼤大汇总起来,此时汇总 起来的数据是有序的。
适合于最大值和最小值的差值不是很⼤的排序。
提示:
1 <= nums.length <= 50000
-50000 <= nums[i] <= 50000
func sortArray(nums []int) []int {
cnt := [100001]int{}
for i := 0; i < len(nums); i++ {
cnt[nums[i] + 50000]++
}
idx := 0
for i := 0; i < 100001; i++ {
for cnt[i] > 0 {
nums[idx] = i - 50000
idx++
cnt[i]--
}
}
return nums
}
复杂度分析
- 时间复杂度:O(n+k)
- 空间复杂度:O(k)
稳定排序
func count_sort(li []int) {
max_num := li[0]
for i := 1; i < len(li); i++ {
if max_num < li[i] {
max_num = li[i]
}
}
arr := make([]int, max_num+1)
for j := 0; j < len(li); j++ {
arr[li[j]]++
}
k := 0
for m, n := range arr {
for p := 0; p < n; p++ {
li[k] = m
k++
}
}
}
9.桶排序
将数据分到有限数量的桶里,每个桶再分别排序
func bin_sort(li []int, bin_num int) {
min_num, max_num := li[0], li[0]
for i := 0; i < len(li); i++ {
if min_num > li[i] {
min_num = li[i]
}
if max_num < li[i] {
max_num = li[i]
}
}
bin := make([][]int, bin_num)
for j := 0; j < len(li); j++ {
n := (li[j] - min_num) / ((max_num - min_num + 1) / bin_num)
bin[n] = append(bin[n], li[j])
k := len(bin[n]) - 2
for k >= 0 && li[j] < bin[n][k] {
bin[n][k+1] = bin[n][k]
k--
}
bin[n][k+1] = li[j]
}
o := 0
for p, q := range bin {
for t := 0; t < len(q); t++ {
li[o] = bin[p][t]
o++
}
}
}
复杂度分析
- 时间复杂度: O(n+k)
- 空间复杂度: O(n+k)
稳定
10.基数排序
先以个位数的⼤小来对数据进⾏排序,接着以十位数的⼤小来对数据进⾏排序,接着以百位数的⼤小…
排到最后,就是一组有序的元素了。不过,他在以某位数进行排序的时候,是⽤用“桶”来排序的。
由于某位数(个位/⼗位…,不是整个数)的⼤小范围为0-9,所以我们需要10个桶,然后把具有相同 数值的数放进同⼀个桶⾥,之后再把桶里的数按照0号桶到9号桶的顺序取出来,这样一趟下来,按照某位数的排序就完成了
func radix_sort(li []int) {
max_num := li[0]
for i := 0; i < len(li); i++ {
if max_num < li[i] {
max_num = li[i]
}
}
for j := 0; j < len(strconv.Itoa(max_num)); j++ {
bin := make([][]int, 10)
for k := 0; k < len(li); k++ {
n := li[k] / int(math.Pow(10, float64(j))) % 10
bin[n] = append(bin[n], li[k])
}
m := 0
for p := 0; p < len(bin); p++ {
for q := 0; q < len(bin[p]); q++ {
li[m] = bin[p][q]
m++
}
}
}
}
复杂度分析
- 时间复杂度: O(kn)
- 空间复杂度: O(n+k)
稳定
本题采用计数排序
func sortArray(nums []int) []int {
cnt := [100001]int{}
for i := 0; i < len(nums); i++ {
cnt[nums[i] + 50000]++
}
idx := 0
for i := 0; i < 100001; i++ {
for cnt[i] > 0 {
nums[idx] = i - 50000
idx++
cnt[i]--
}
}
return nums
}
参考资料:
https://leetcode-cn.com/problems/sort-an-array/solution/golang-by-xilepeng-2/
