语法解析一个非常重要的功能就是要构建一个树形数据结构,也叫语法解析树,无论是解释器执行当前语句还是编译器将语句转换为低级语言,解析树都是一个承上启下的重要结构。对任何生产式A -> X Y Z,它都会生成一个以A为父节点,X,Y,Z为子节点的多叉树,而且X,Y,Z作为节点出现的顺序与他们在生产树中出现的位置一样,如下图所示:
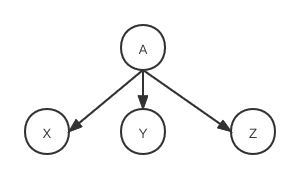
所有非终结符都会成为解析树的中间节点,而所有终结符都会成为叶子节点。对于算术表达式9-5+2, 由于我们会首先使用list -> list + digit 来进行解析,因此 9-5对应一个list,2对应digit,
因此最终解析完成后,所形成的解析树如下:
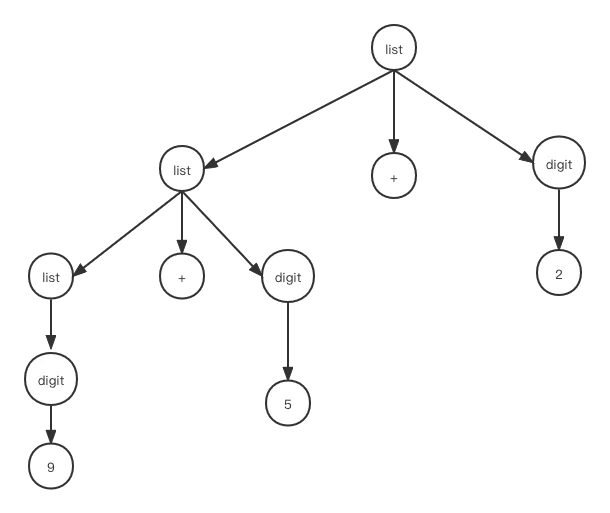
使用生产式来定义语法是一件困难的事情,做不好就会产生歧义性,例如在前面的生产式中,我们不使用digit-> “0” | “1” …“9”,而是使用list->“0”,“1”…“9”,于是生产式为:
list -> list + list
list -> list - list
list-> "0" | "1" ..."9"
于是在解析9-5+2时就会有两种情况,一种是使用list->list+list进行解析,一种是使用list->list-list进行解析,如果是后者,那么我们会生成的语法树如下:
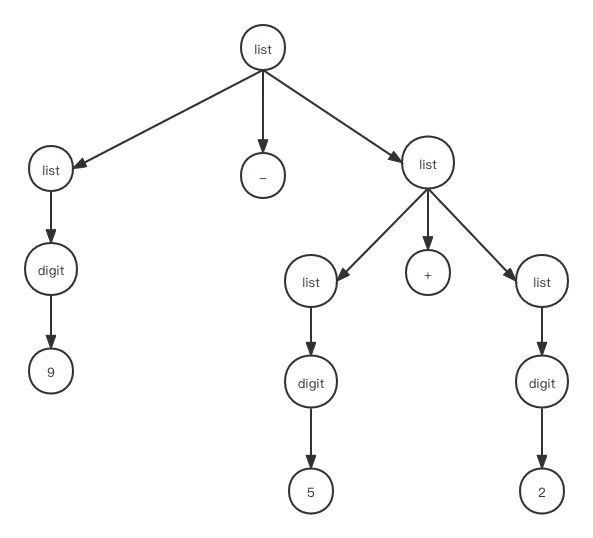
这里我们看到两个语法表达式都对应表达式"9-5+2",但是第一个语法树执行的操作时(9-5)+2也就是结果为6,第二个语法书执行的操作是9-(5+2),所得结果是2,因此不同的语法树会导致不同的操作结果。因此在语法有歧义的情况下,虽然给定的字符串能通过解析,但是后续操作,例如生成中间代码,或是解释器要解释执行语句时就会有问题,因为它不知道应该用哪一种语法树为基础,于是前面几节我们设定的语法生产式就存有歧义。
为了避免产生歧义,我们将前面的语法生产式修改如下:
list -> "(" list + ")"
list -> list "+" NUM
list -> list "-" NUM
NUM -> "0"|"1"...|"9"
经过上面的修改后,我们在解析时就不会产生两种不同的语法树。在此我们先将错就错,继续按照前面描述的解析方式去构造语法树,后面章节我们再给出解决办法。
此外语法解析树之所以作用很大,是因为我们可以给每个节点赋予一些属性,以及基于属性的特点操作,当我们遍历完整个解析树,并针对每个节点执行它对应的操作后,我们会得到很好的结果,后面我们会看到中间代码的生成就依赖于这种方法。为了简单起见,我们先看一种特定情况:后项表达式。
后项表达式的定义如下:
1, 如果E表示一个变量或者常量,那么它对应的后项表达式就是它自己。
2,如果E是一个具有这种格式的算术表达式 E1 op E2, 其中op是对应两个操作数的运算符,那么E的后项表达式为E1’ E2’ op, 其中E1’是E1的后项表达式,E2’是E2的后项表达式
3,如果E是带有括号的算术表达式,也就是E=(E1),那么E的后项表达式就是去掉括号,然后获取E1的后项表达式。
上面定义看起来比较抽象,我们看一些具体例子,例如10, a,他们对应的后项表达式就是自身。对于算术表达式1+2,对应的算术表达式就是1 2 +, 对于表达式(3+4),对应的后项表达式就是3 4 + , 我们看一个复杂一点的,(9-5)+2 ,首先我们计算(9-5)的后项表达式,也就是9 5 -,接下来我们再套用第二点,于是变成9 5 - 2 +.
现在我们给语法树上每个节点赋予一个字符串属性叫t,同时我们在给出语法生生产式时,也给出对应节点属性的生成规则如下:
list -> list "+" digit (list.t = list.t || digit.t || "+")
list -> list "-" digit (list.t = list.t || digit.t || "-")
digit -> "0" (digit.t = "0")
digit -> "1" (digit.t = "1")
...
digit -> "9" (digit.t = "9")
在上面表达式中,右边括号的内容叫“语义规则”,其中符号||表示将字符串相连接,上面的理论描述比较抽象,接下来我们看看代码实现,由此来将理论进行具体化理解,首先我们先增加语法树节点的定义,在parser目录下增加一个文件叫syntax_node.go,添加内容如下:
package simple_parser
type NodeInterface interface {
AddChild(child NodeInterface)
GetChildren() []NodeInterface
Attribute() string
}
type SyntaxNode struct {
T string
children []NodeInterface
}
func NewSyntaxNode() *SyntaxNode {
return &SyntaxNode{
T: "",
}
}
func (s *SyntaxNode) AddChild(node NodeInterface) {
s.children = append(s.children, node)
}
func (s *SyntaxNode) GetChildren() []NodeInterface {
return s.children
}
func (s *SyntaxNode) Attribute() string {
if len(s.children) == 0 {
return s.T
}
attribute := ""
for _, child := range s.children {
//根据语义规则,父节点的属性是将所有子节点的属性连接后再添加父节点对应的操作符
attribute = attribute + child.Attribute()
}
attribute += s.T
return attribute
}
然后在原来list_parser.go中做如下代码修改:
package simple_parser
import (
"errors"
"io"
"lexer"
)
type SimpleParser struct {
lexer lexer.Lexer
}
func NewSimpleParser(lexer lexer.Lexer) *SimpleParser {
return &SimpleParser{
lexer: lexer,
}
}
func (s *SimpleParser) list() (*SyntaxNode, error) {
//根据读取的第一个字符决定选取哪个生产式
token, err := s.lexer.Scan()
if err != nil {
return nil, err
}
current_list_node := NewSyntaxNode() //newly add
if token.Tag == lexer.LEFT_BRACKET {
//选择 list -> ( list )
child_list_node, err := s.list() //newly add
if err != nil { //newly add
return nil, err
}
if child_list_node != nil {
current_list_node.AddChild(child_list_node) //newly add , add child noe
}
token, err = s.lexer.Scan()
if token.Tag != lexer.RIGHT_BRACKET {
err := errors.New("Missinf of right bracket")
return nil, err
}
}
if token.Tag == lexer.NUM {
// list -> number
child_list_node := NewSyntaxNode()
child_number_node, err := s.number() // newly add
if child_number_node != nil {
child_list_node.AddChild(child_number_node)
current_list_node.AddChild(child_list_node)
}
if err != nil {
if err == io.EOF {
return current_list_node, err
}
return nil, err
}
}
token, err = s.lexer.Scan()
if err != nil {
if err == io.EOF {
return current_list_node, err
}
return nil, err
}
if token.Tag == lexer.PLUS || token.Tag == lexer.MINUS {
current_list_node.T = s.lexer.Lexeme
child_list_node, err := s.list() // list -> list + list , list -> list - list
if child_list_node != nil {
current_list_node.AddChild(child_list_node)
}
if err != nil {
if err == io.EOF {
return current_list_node, err
}
return nil, err
}
} else {
s.lexer.ReverseScan()
}
return current_list_node, nil
}
func (s *SimpleParser) number() (*SyntaxNode, error) {
if len(s.lexer.Lexeme) > 1 {
err := errors.New("Number only allow 0-9")
return nil, err
}
current_node := NewSyntaxNode()
current_node.T = s.lexer.Lexeme
return current_node, nil
}
func (s *SimpleParser) Parse() (*SyntaxNode, error) {
return s.list()
}
最后在main.go中完成代码如下:
package main
import (
"fmt"
"io"
"lexer"
"simple_parser"
)
func main() {
source := "9-5+2"
my_lexer := lexer.NewLexer(source)
parser := simple_parser.NewSimpleParser(my_lexer)
root, err := parser.Parse()
if err == io.EOF {
fmt.Println("Syntax translation: ", root.Attribute())
} else {
fmt.Println("source is legal expression")
}
}
在上面代码中,我们构建了第二个图对应的解析树,同时为每个节点设置了对应的属性,如下图所示:
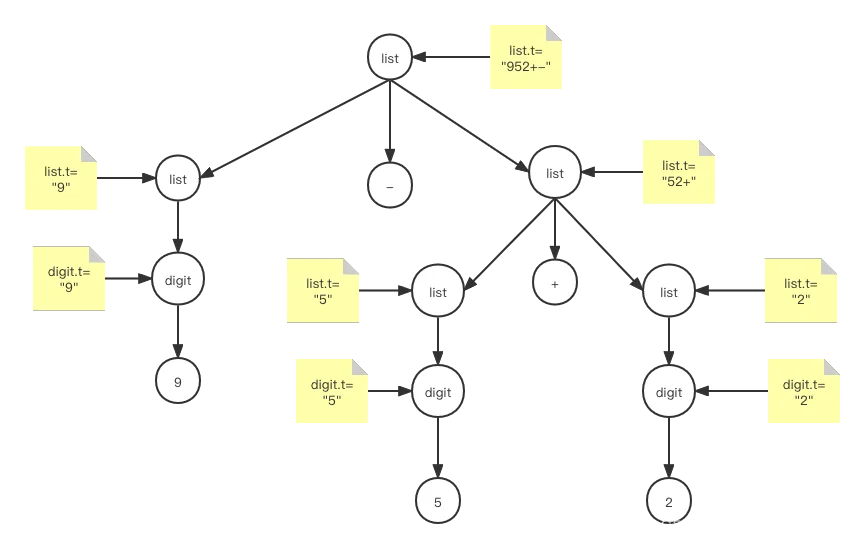
代码运行后输出的结果也是“952±”,按理“9-5+2"对应的后项表达式应该是"95-2+",由于我们原来定义的语法具有歧义性,我们通过语法解析树获得的后项表达式并不准确,这个问题在后面我们进一步分析语法解析流程时会解决.由于代码有多处修改,因篇幅所限,这里我只给出了一小部分,完整代码这里下载:https://github.com/wycl16514/dragon-compiler-syntax-tree.git,更详细的讲解和调试演示,请在B站搜索Coding迪斯尼。
