堆原理解析
堆一般指二叉堆。是使用完全二叉树这种数据结构构建的一种实际应用。通过它的特性,分为最大堆和最小堆两种。
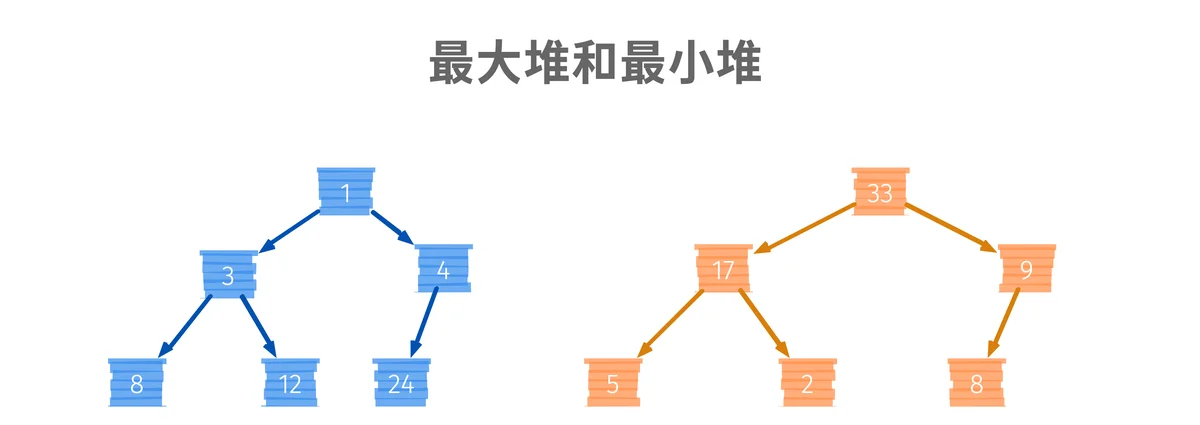
如上图可知,最小堆就是在这颗二叉树中,任何一个节点的值比其所在子树的任意一个节点都要小。最大堆就是在这颗二叉树中,任何一个节点的值都比起所在子树的任意一个节点值都要大。
那么如何构建一个堆呢?首先要将所有的元素构建为一个完全二叉树。完全二叉树是指除叶子节点,所有层级是满节点,叶子节点从左向右排列填满。
在一个完全二叉树中,将数据重新按照堆的的特性排列,就可以将完全二叉树变成一个堆。这个过程叫做“堆化”。
在堆中,我们要删除一个元素一般从堆顶删除(可以取到最大值/最小值)。删除之后,数据集就不能算作一个堆了,因为最顶层的元素没有了,数据集不符合完全二叉树的定义。这时,我们需要将堆的数据进行重新排列,也就是重新“堆化”。同样的,在堆中新添加一个元素也需要重新做“堆化”的操作,来将数据集恢复到满足堆定义的状态。
所以,在堆这种数据结构中,最重要的是“堆化”的这个算法操作。其次,堆化数据如何存储也是很重要的。接下来,详细说一下。
完全二叉树的存储方式
对于二叉树来说,存储方式有2种,一种使用数组的形式来存储,一种使用链表的方式存储。同样的,这两种方式继承了这两种数据结构的坏处和好处。链表的方式相对浪费存储空间,因为要存储左右子树的指针,但扩缩容方便。而数组更加节省空间,更加方便定位节点,缺点则是扩缩容不便。
我们以数组的方式来做示例,了解存储的细节:
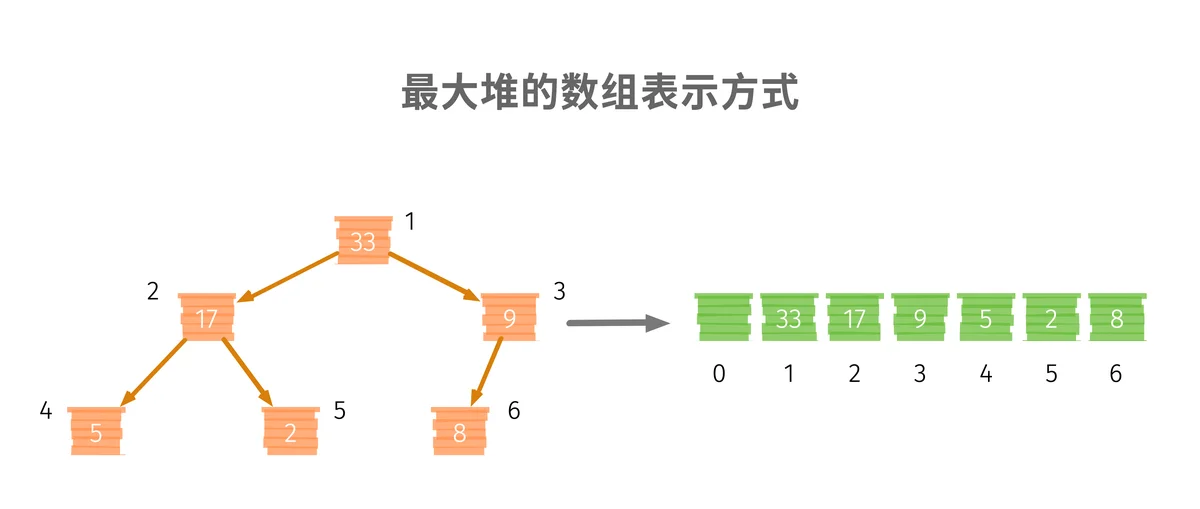
我们不用 \(index = 0\) 的位置来存储数据,而是从 \(index = 1\) 开始,这样,对于任意一个节点 \(i\) 来说,就有 左节点 \(2*i\),右节点 \(2*i+1\),而父节点就是 \(\frac i 2\)。
堆的操作
我们先介绍两种常用的堆操作:pop & push,添加一个元素和删除一个元素。
假如我们有如下的一个最大堆,当我们添加了一个元素之后,就需要做“堆化”,使得堆满足定义。
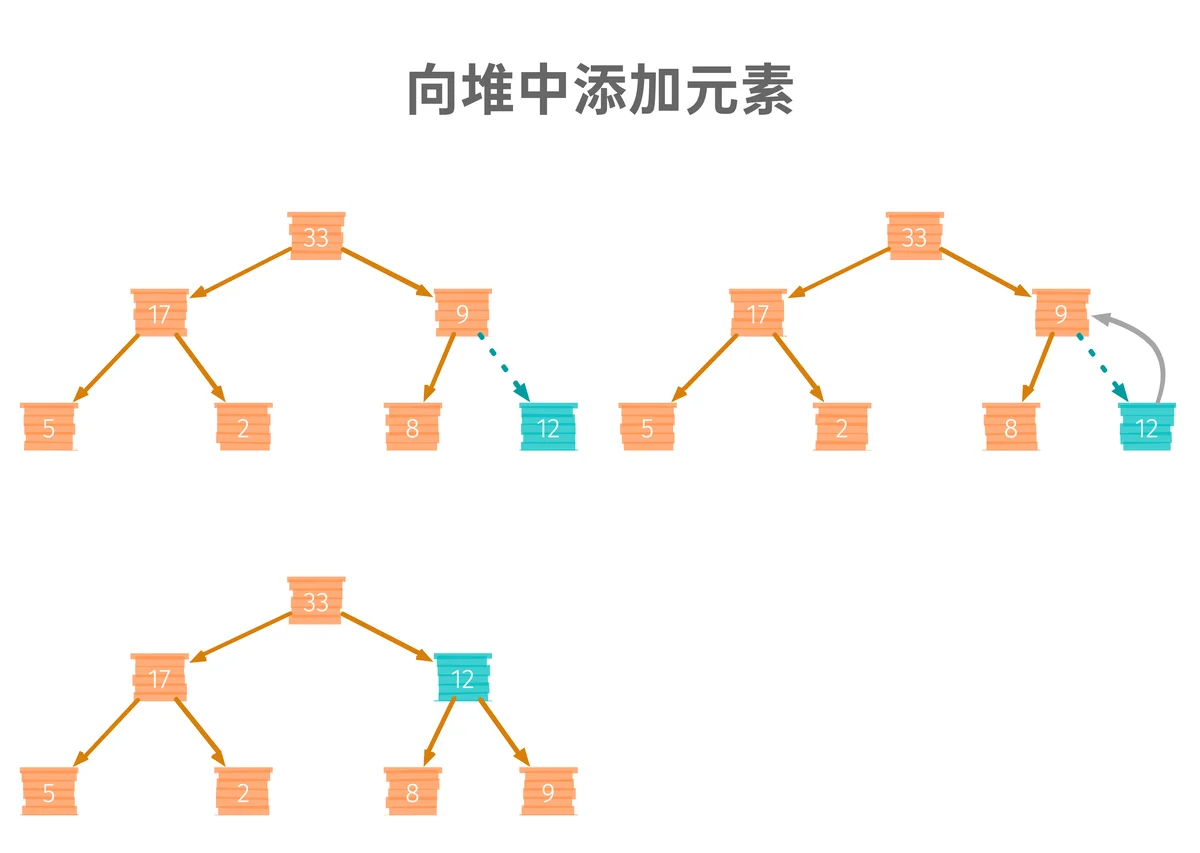
这种从堆底向上堆化的过程,叫做“从下到上堆化”。我把这个过程实现为代码,如下:
// 从下到上堆化
func (h *Heap) downToUpHeapify(pos int) {
for pos / 2 > 0 && h.data[pos/2].Less(h.data[pos]) { // 如果存在父节点 & 值大于父节点
h.swap(pos, pos/2) // 交换两个值的位置
pos = pos /2 // 将操作节点变为父节点的位置
}
}
当我们想要从堆顶 pop 一个元素的时候。我们需要先将元素pop,然后把堆中最后一个元素放到堆顶,然后进行一次“堆化”。
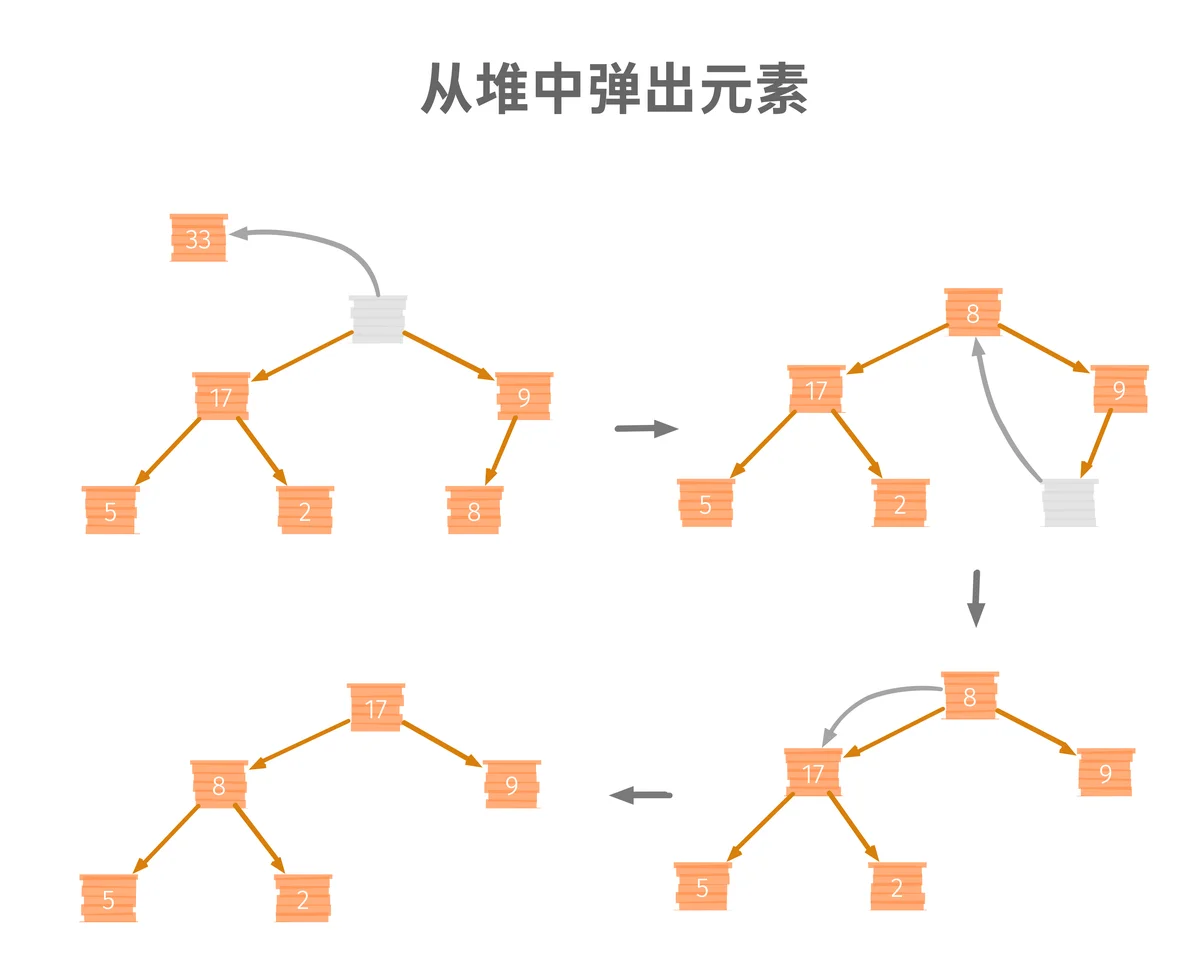
这种从堆顶向下堆化的过程,叫做“从上到下堆化”。我把这个过程实现为代码,如下:
// 从上到下堆化
func (h *Heap) upToDownHeapify() {
max := h.len
i := 1
pos := i
for {
if i * 2 <= max && h.data[i].Less(h.data[i*2]) { // 如果有左子树,且自己小于左子树
pos = i*2
}
if i *2 +1 <= max && h.data[pos].Less(h.data[i*2+1]) { // 如果有右子树,且自己小于右子树
pos = i*2+1
}
if pos == i { // 如果位置没有变化,说明堆化结束
break
}
h.swap(i, pos) // 交换当前位置和下一个位置的内容
i = pos // 操作下一个位置
}
}
Golang 的 container.heap 包
注意,上述的讲述中,为了方便表示,我们在数组的索引0没有存储内容,从索引1开始存储。
而 Golang 的实现中,索引0 是存储了数据的。这样的话,每一个元素的左子树和右子树就分别变成了 \(2*i+1\) 和 \(2*i+2\)。
Interfacetype Interface interface {
sort.Interface
Push(x interface{}) // 把元素添加到 Len() 的位置
Pop() interface{} // 删除并返回 Len() - 1 的元素.
}
// sort.Interface
type Interface interface {
// Len is the number of elements in the collection.
Len() int
// Less reports whether the element with
// index i should sort before the element with index j.
Less(i, j int) bool
// Swap swaps the elements with indexes i and j.
Swap(i, j int)
}
sort.InterfacePushPopsort.InterfaceLenLessSwap接下来,我们看一下 Push 操作:
func Push(h Interface, x interface{}) {
h.Push(x) // 向数据集添加一个元素
up(h, h.Len()-1) // 从下向上堆化
}
// 从下向上堆化的内容
func up(h Interface, j int) {
// h 表示堆,j 代表需要堆化的元素 index
for {
i := (j - 1) / 2 // 定义 j 的父 index
if i == j || !h.Less(j, i) { // 如果两个元素相等 或者 父元素小于当前元素
break // 堆化完成
}
h.Swap(i, j) // 交换父元素和当前元素
j = i // index 变为父元素的 index
}
}
上面在 push 元素之后,做了 “从下到上”的堆化。
接下来,是 Pop 操作:
// 返回堆顶的元素,并删掉它
func Pop(h Interface) interface{} {
n := h.Len() - 1 // 获取最终堆长度(去掉最后一个元素)
h.Swap(0, n) // 交换堆顶和最后一个元素
down(h, 0, n) // 从上到下堆化
return h.Pop() // 弹出最后一个元素
}
func down(h Interface, i0, n int) bool {
i := i0 // 堆顶 index
for {
j1 := 2*i + 1 // 左孩子 index
if j1 >= n || j1 < 0 { // j1 大于堆长度 或 溢出
break // 堆化结束
}
j := j1 // j = 左孩子
if j2 := j1 + 1; j2 < n && h.Less(j2, j1) {
// j2 = 右孩子;j 小于堆长度 && 右孩子小于左孩子
j = j2 // j = 2*i + 2 = 右孩子
}
// 上面是从左右孩子选出小的那个,将 index 赋值给 j
if !h.Less(j, i) { // 如果 堆顶小于 j , 堆化结束
break
}
h.Swap(i, j) // 交换堆顶元素和 j
i = j // 切换到下一个操作 index
}
// 返回 元素是否有移动
// 此处是一个特殊设计,用来判断向下堆化是否真的有操作
// 当删除中间的元素时,如果向下堆化没有操作的话,就需要再做向上堆化
return i > i0
}
RemoveFixRemoveFixfunc Remove(h Interface, i int) interface{} {
n := h.Len() - 1 // 堆的长度
if n != i { // 如果不是堆顶
h.Swap(i, n) // 交换删除元素 和 最后一个元素
if !down(h, i, n) { // 从上到下堆化
up(h, i) // 如果没有成功,就从下岛上堆化
}
}
return h.Pop() // 弹出最后一个元素
}
func Fix(h Interface, i int) {
// i 是值被改变的 index
if !down(h, i, h.Len()) { // 从上到下堆化
up(h, i) // 如果没有成功,就从下岛上堆化
}
}
RemoveFixRemoveInitfunc Init(h Interface) {
n := h.Len() // n 是堆长度
// i = 最后一个非叶子节点的 index; i >= 堆顶; index 自减
for i := n/2 - 1; i >= 0; i-- {
// 从当前节点开始,从上到下堆化
down(h, i, n)
}
}
根据堆的特性可知,叶子节点不可以从上到下堆化。所以,我们找到最后非叶子节点的索引值,从这里开始做堆化操作。
container.heap堆的应用
在堆排序中,就需要用到堆算法来将数据级堆化,然后一个个的弹出元素,以达到排序的目的。
堆也可以用于实现优先级队列。优先级队列在实际开发过程中有着广泛的应用。在很多时候,都可以用它来实现处理带优先级的事件,处理定时任务等等。
