I.内容提要 定时调度系统(定时任务、定时执行)算是工作中经常依赖的中间件系统,简单使用操作系统的 crontab,或基于 Quartz,xxl-job 来搭建任务调度平台,行业有很多优秀的开源产品和中间件。 了解其工作和设计原理,有助于我们完善或定制一套适合公司业务场景的任务调度中间件,之前写了两篇文章介绍了调度负载均衡和定时延时任务的内容,可以参考。贺鹏 目前就职某互联网金融公司负责架构及开发管理工作,在分布式领域和风控领域深入研究。
- 分布式调度分发负载均衡及服务保持
- 分布式调度延时任务实现原理
- 任务调度依赖 & 工作流
图相关知识
golang 并发相关
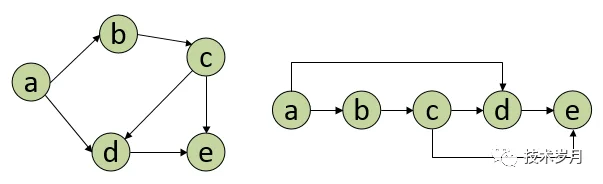
什么是任务依赖?比如 “任务 a” 执行的前提是 “任务 b” 先执行完成,“任务b” 又依赖于 “任务 c” 先执行,那么就形成如下依赖关系。
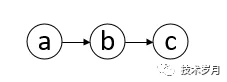
这个还比较简单,如果复杂点的如下图所示,形成一个工作流,Azkaban 大数据调度器就实现了工作流模式调度依赖,这是一个典型的图应用案例。
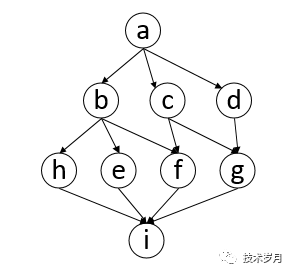
III.图数据结构
提到图数据结构,大部分人既熟悉又陌生,因为大学基本都学过,但一般工作场景都不会用到,这里就先简单回顾一下图相关的知识。
图 graph ,图中的元素称为顶点 vertex。图中任一顶点可以与其他顶点建立连线关系,叫做边 edge。
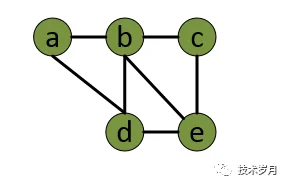
上面图叫 “无向图”,如果边有 “方向” ,那么就是 “有向图” 了。
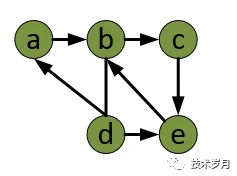
无向图中,顶点有几条边就叫几度;有向图中,顶点有入度,表示有多少边指向此顶点,顶点的出度表示该顶点有多少边指向 “远方” 。
上图中 a 指向 b,b 指向 d,d 又指向 a, a、b、d 之间形成一个环,如果将顶点比作调度的任务,那么任务 a 完成必须依赖任务 b,任务 b 又依赖任务 d,任务 d 又依赖任务 a,那么最终肯定无法完成,因此调度问题使用的是有向无环图 (DAG),比如我们最早那张图。

了解了图的基本概念,那么图结构如何用代码表示出来?这里涉及到图的两种存储方式:邻接矩阵、邻接表。
邻接矩阵底层为二维数据,如果有一条边顶点为 x 和 y,对无向图来说,对应的数据 Array[x][y] 和 Array[y][x] 标记为 1;对有向图 x->y ,只将 Array[x][y] 标记为 1 即可,下图为使用邻接矩阵表示的无向图和有向图。
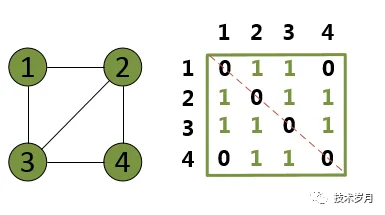
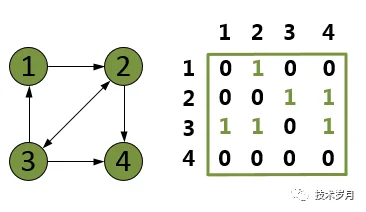
对于无向图来说,邻接矩阵沿着红色对角线两边是对称的,如果图的顶点连线比较少,这种叫稀疏图,将存储大量的 0 ,浪费存储空间,这时候可以选择使用邻接表表示,相对稀疏图的叫稠密图,使用邻接矩阵可以更好地查询连通性,其原理也是用空间换时间。下图为使用邻接表表示的无向图和有向图。
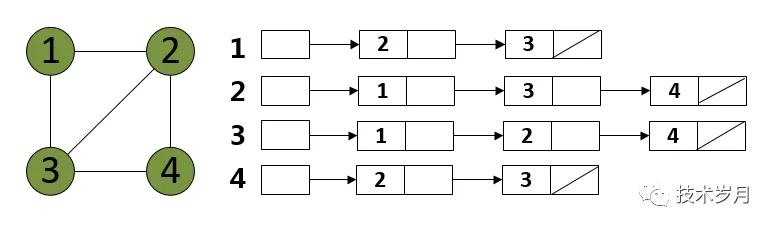
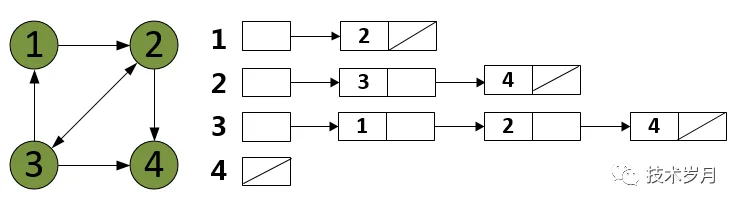
最后说下图的遍历,和遍历树一样分为广度优先 BFS 和 深度优先 DFS,但图如果存在成环的情况,访问的节点要做记录,同时可用辅助队列存放待访问的邻接节点。
拓扑排序,对有向无环图的顶点进行遍历,将所有顶点形成一个线性序列,可以用数组(切片)或链表存储,如下图。
IV.golang 代码实现
回顾了图的相关知识,那么回到最开始的任务依赖工作流中,将每个任务看成图的顶点,任务 a 依赖 任务 b,使用一条有向线从 a 指向 b,最后将所有任务顶点连线形成一个图,这个图是一个有向无环图 DAG,对 DAG 进行拓扑排序,形成一个任务执行链表,反向执行即可解决依赖问题。

首先定义一个图结构体,这里使用邻接矩阵方式存储,图的顶点结构体存储 Key 和 Value 代表任务的相关执行信息。
//图结构type DAG struct { Vertexs []*Vertex}//顶点type Vertex struct { Key string Value interface{} Parents []*Vertex Children []*Vertex}为图添加顶点和添加边,这里是有向图,from 代表边的起始顶点, to 代表边的终止顶点。
//添加顶点func (dag *DAG) AddVertex(v *Vertex) { dag.Vertexs = append(dag.Vertexs, v)}//添加边func (dag *DAG) AddEdge(from, to *Vertex) { from.Children = append(from.Children, to) to.Parents = append(to.Parents, from)}建立 a - i 所有顶点,再对每个顶点连线。
var dag = &DAG{}//添加顶点va := &Vertex{Key: "a", Value: "1"}vb := &Vertex{Key: "b", Value: "2"}vc := &Vertex{Key: "c", Value: "3"}vd := &Vertex{Key: "d", Value: "4"}ve := &Vertex{Key: "e", Value: "5"}vf := &Vertex{Key: "f", Value: "6"}vg := &Vertex{Key: "g", Value: "7"}vh := &Vertex{Key: "h", Value: "8"}vi := &Vertex{Key: "i", Value: "9"}//添加边dag.AddEdge(va, vb)dag.AddEdge(va, vc)dag.AddEdge(va, vd)dag.AddEdge(vb, ve)dag.AddEdge(vb, vh)dag.AddEdge(vb, vf)dag.AddEdge(vc, vf)dag.AddEdge(vc, vg)dag.AddEdge(vd, vg)dag.AddEdge(vh, vi)dag.AddEdge(ve, vi)dag.AddEdge(vf, vi)dag.AddEdge(vg, vi)对该图进行广度优先遍历,通过引入队列来减少时间复杂度,遍历后生成一个包含所有顶点的 slice 。
选择起始节点入队列
节点出队列
2.1 队列空了,说明遍历完毕返回 2.2 已访问跳过,未访问顶点放入输出 slice 中
2.3 将节点的所有未访问邻接节点 Children 放入队列3. 重复执行 2
注意 slice 加入顺序,因为执行要从 i 到 a 的顺序,所以将每次遍历后的元素放到 slice 第一个位置。
func BFS(root *Vertex) []*Vertex { q := queue.New() q.Add(root) visited := make(map[string]*Vertex) all := make([]*Vertex, 0) for q.Length() > 0 { qSize := q.Length() for i := 0; i < qSize; i++ { //pop vertex currVert := q.Remove().(*Vertex) if _, ok := visited[currVert.Key]; ok { continue } visited[currVert.Key] = currVert all = append([]*Vertex{currVert}, all...) for _, val := range currVert.Children { if _, ok := visited[val.Key]; !ok { q.Add(val) //add child } } } } return all}最后就是对所有任务进行执行,这里假定每个任务执行需要 5 秒,然后输出执行结果。
func doTasks(vertexs []*Vertex) { for _, v := range vertexs { time.Sleep(5 * time.Second) fmt.Printf("do %v, result is %v \n", v.Key, v.Value) }}
通过执行测试用例,可以看到执行按上述生成的 slice 顺序,从左向右逐个执行,满足任务依赖关系。
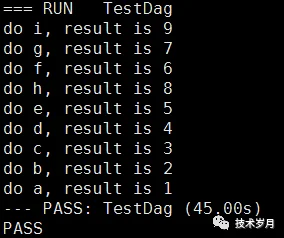
但这里有个问题就是执行时间过长,因为每一个都是串行执行,9 个任务要执行 45 秒。那么并行不就解决了?但任务有依赖关系又如何并行呢?
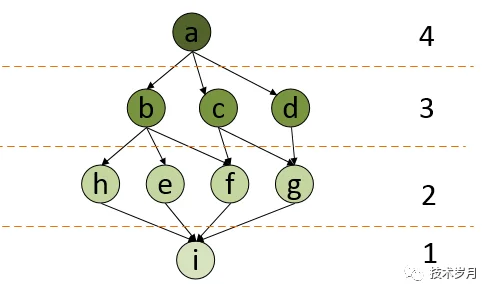
通过这个图即可一目了然明白了,分层执行,上层任务依赖下层,但每一层的任务相互独立可以并发执行。
首先在 BFS 遍历生成顶点的时候,需要生成双层切片:
[0] [] { i }
[1] [] { h, e, f, g }
[2] [] { b, c, d }
[3] [] { a }
func BFSNew(root *Vertex) [][]*Vertex { q := queue.New() q.Add(root) visited := make(map[string]*Vertex) all := make([][]*Vertex, 0) for q.Length() > 0 { qSize := q.Length() tmp := make([]*Vertex, 0) for i := 0; i < qSize; i++ { //pop vertex currVert := q.Remove().(*Vertex) if _, ok := visited[currVert.Key]; ok { continue } visited[currVert.Key] = currVert tmp = append(tmp, currVert) for _, val := range currVert.Children { if _, ok := visited[val.Key]; !ok { q.Add(val) //add child } } } all = append([][]*Vertex{tmp}, all...) } return all }同时执行时候按每一层并发执行。这里通过 sync.WaitGroup 保障并发同步等待。
for _, layer := range all { fmt.Println("------------------") doTasksNew(layer)}//并发执行func doTasksNew(vertexs []*Vertex) { var wg sync.WaitGroup for _, v := range vertexs { wg.Add(1) go func(v *Vertex) { defer wg.Done() time.Sleep(5 * time.Second) fmt.Printf("do %v, result is %v \n", v.Key, v.Value) }(v) //notice } wg.Wait()}上述代码注意,遍历变量被并发调度必须进行绑定,如果按下面这样写将会有问题。
for _, v := range vertexs {
go func() {
//...
fmt.Printf(v)
}()
}
这是因为 for k, v := rang xx 语句中,每次循环变量 k 和 v 是重新赋值,并非生成新的变量,如果循环中启动协程并引用变量 k 和 v 很可能在循环结束时才开启协程执行,这时所有协程中的变量 k 和 v 都是同一个变量,输出内容也会完全相同。所以这里将 v 加入函数参数中,因为 go 函数都是值传递,会重新绑定到新的变量中。
通过并发改造后,执行时间只有 20 秒了,大大提高了任务执行的效率。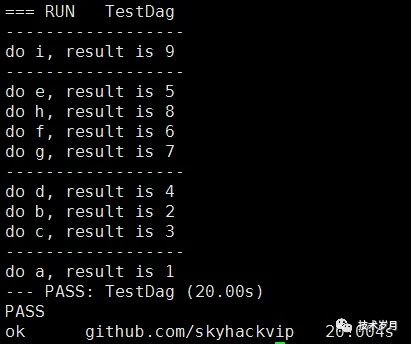
通过本章内容,我们实现了任务调度的工作流模式,本文代码可访问 https://github.com/skyhackvip/dag 更多了解。
参考阅读:领域驱动设计框架Axon实践
用 Golang 快速实现 Paxos 分布式共识算法
Java内存模型深入分析
阿里双11同款流控降级组件 Sentinel Go简介
改善 Java 代码质量的工具与方法
Java 语言中锁的设计与应用
技术原创及架构实践文章,欢迎通过公众号菜单「联系我们」进行投稿。
高可用架构 改变互联网的构建方式
